I numeri naturali preceduti dal segno + formano l'insieme
dei numeri interi positivi che si indica con Z+.
I numeri naturali preceduti dal segno — formano l'insieme
dei numeri interi negativi che si dica con Z-
I due insiemi Z+ e Z- formano
complessivamente l'insieme dei numeri interi che si indica con Z.
Il valore assoluto di un numero intero relativo è il numero senza il segno: quindi un numero naturale.
Il valore assoluto si indica inserendo il numero relativo tra due barre verticali.
Numeri aventi lo stesso segno si dicono CONCORDI:
+3 e +6 sono concordi
-5 e -1 sono concordi
Numeri con
segno fra loro diverso si dicono DISCORDI:
+4 e -5 sono discordi
-4 e +2 sono discordi
Due numeri interi relativi sono uguali se hanno lo stesso segno e lo stesso valore assoluto.
Due numeri discordi ma con lo stesso
valore assoluto si dicono OPPOSTI o contrari o simmetrici:
sono numeri opposti +3 e -3; +9 e -9; +10 e -10.
Attenzione
Per indicare un numero positivo è possibile scrivere il numero senza il segno +.
Per esempio si può scrivere indifferentemente +1 o 1, +11 o semplicemente 11.
CONFRONTO
1) Qualsiasi numero positivo è maggiore di un qualsiasi numero
negativo.
+5 > -17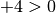
2) Lo zero è minore di ogni numero positivo e maggiore di ogni numero negativo.
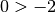
3) Fra due numeri positivi è maggiore quello che ha maggior valore assoluto.
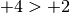
i numeri sono positivi, il maggiore è +4 perché ha valore assoluto maggiore.
4) Fra due numeri negativi è maggiore quello che ha minor
valore assoluto.
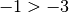
i due numeri sono negativi, il maggiore è -1 perché ha valore assoluto
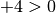
2) Lo zero è minore di ogni numero positivo e maggiore di ogni numero negativo.
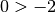
3) Fra due numeri positivi è maggiore quello che ha maggior valore assoluto.
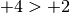
i numeri sono positivi, il maggiore è +4 perché ha valore assoluto maggiore.
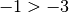
i due numeri sono negativi, il maggiore è -1 perché ha valore assoluto
ADDIZIONE
La somma di due numeri interi relativi concordi è un numero
intero concorde ad essi e avente per valore assoluto la somma dei valori
assoluti.
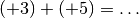
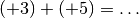
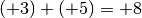 .
.
Esempio 2
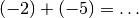
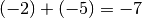 .
.La somma di due numeri interi relativi discordi è un numero intero concorde all'addendo che ha maggior valore assoluto e avente per valore assoluto la differenza dei valori assoluti.
Esempio 1
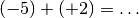
i due numeri da sommare sono discordi, i loro valori assoluti sono 5 e 2, la differenza è 3, il numero che ha valore assoluto maggiore è -5, pertanto il risultato ha lo stesso segno di -5, cioè è negativo, quindi:
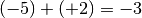 .
.
Esempio 2
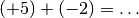
(-7) + (+7) = 0
SOTTRAZIONE
La differenza fra due numeri interi si ottiene addizionando
al primo l'opposto del secondo.
(-7) - (+9) = (-7) + (-9) = -16
(-7) - (+9) = (-7) + (-9) = -16
MOLTIPLICAZIONE
Il prodotto di due numeri interi è un numero che ha per
valore assoluto il prodotto dei val assoluti ed è positivo se i due numeri sono
concordi, negativo se i due numeri sono discordi.
DIVISIONE
Il quoziente di due numeri interi è un numero che ha per
valore assoluto il quoziente dei lori valori assoluti ed è positivo se i due
numeri sono concordi, negativo se i due numeri sono discordi.
Numeri interi relativi (generalità, confronto, addizione algebrica)
Esercizi Confronto tra numeri interi relativi
Esercizi espressioni
Esercizi espressioni da UbiMath di Ubaldo Pernigo